Aspects of Thermal QCD Phenomenology at Intermediate Gauge/'t Hooft Coupling: Appendix C

Table of Links

Abstract

Acknowledgment

PART I

Chapter 1: Introduction

Chapter 2: SU(3) LECs from Type IIA String Theory

Chapter 3: Deconfinement Phase Transition in Thermal QCD-Like Theories at Intermediate Coupling in the Absence and Presence of Rotation

Chapter 4: Conclusion and Future Outlook

PART II

Chapter 5: Introduction

Chapter 6: Page Curves of Reissner-Nordström Black Hole in HD Gravity

Chapter 7: Entanglement Entropy and Page Curve from the M-Theory Dual of Thermal QCD Above Tc at Intermediate Coupling

Chapter 8: Black Hole Islands in Multi-Event Horizon Space-Times

Chapter 9: Multiverse in Karch-Randall Braneworld

Chapter 10: Conclusion and Future outlook

APPENDIX A

APPENDIX B

APPENDIX C

Bibliography

APPENDIX C

C.1 Complex Extrinsic Curvatures and Riemann Tensors

We can go from complex Riemann tensors to real Riemann tensors by using the following coordinate transformations:

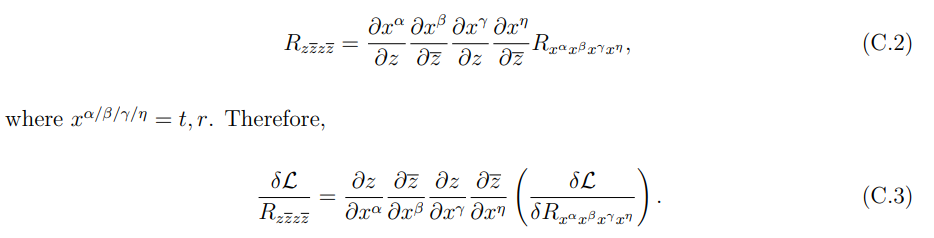
Similarly to calculate the second term is holographic entanglement entropy formula we use the following coordinate transformations:

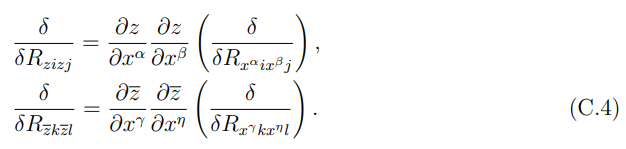
Hence by using equation (C.4) we can obtain the second term appearing in holographic entanglement entropy formula in terms of the real coordinates (t, x) using the coordinate transformations given below:

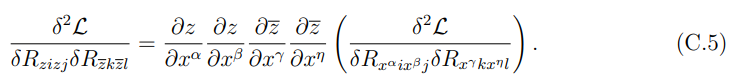
C.2 HM-Like/IS Analytics/Numerics

In the present appendix, we describe (i) the angular integrations utilized throughout the computation and the equation describing the area of a Hartman-Maldacena-like surface, and (ii) the process by which we estimate the turning point in the context of Island Surface entanglement entropy.

C.2.1 HM-Like Surface Area

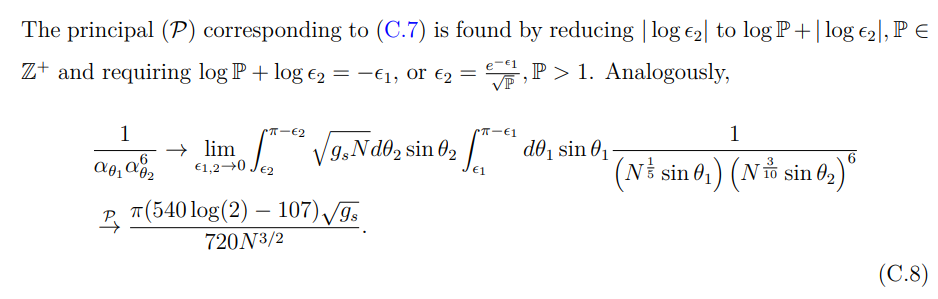
C.2.2 IS Turning Point

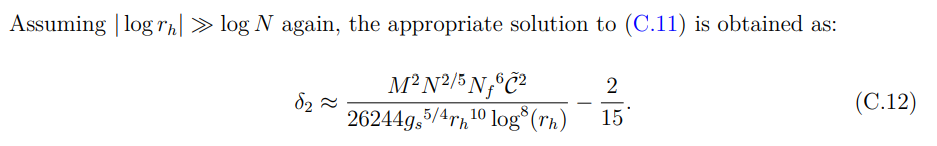
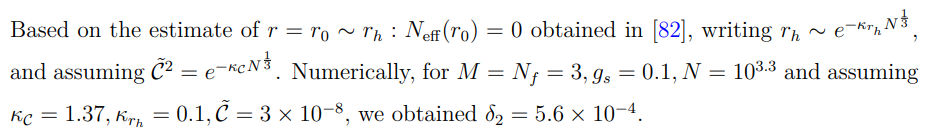
C.3 Hartman-Maldacena-like Surface Miscellania

We present numerous r dependent functions that appear in the entanglement entropy formula to describe the Hartman-Maldacena-like surface at O(β 0 ) and O(β) in this appendix. We also calculated the equation of motion pertaining to the embedding function associated with the Hartman-Maldacena-like surface.

• The r dependent functions appearing in equation (7.57) are given as:

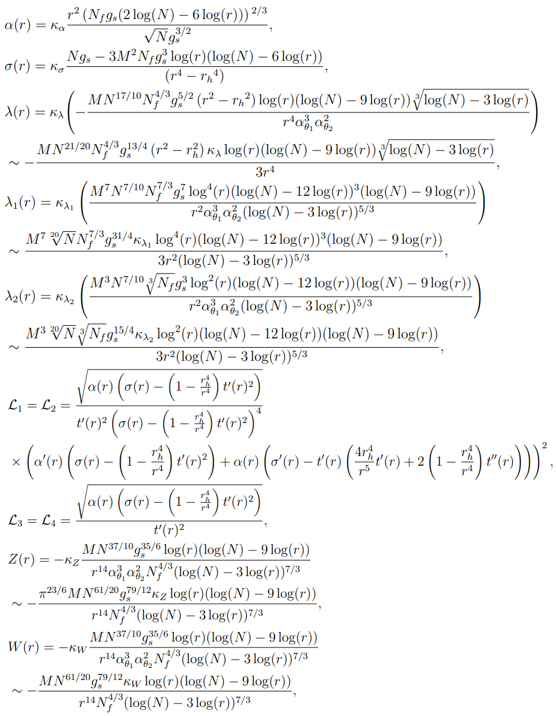
• In the case of the existence of higher derivative terms, the following have been used to compute the first and second terms of holographic entanglement entropy computation:

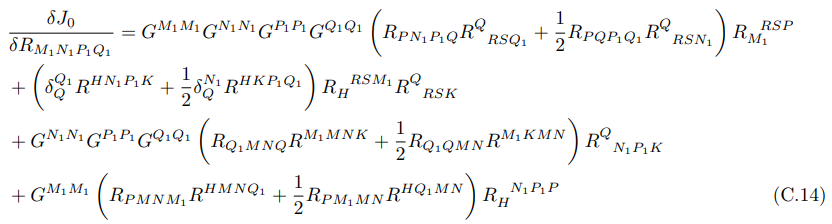
and

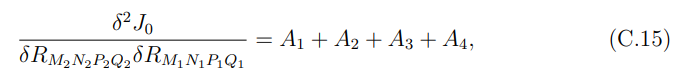
where

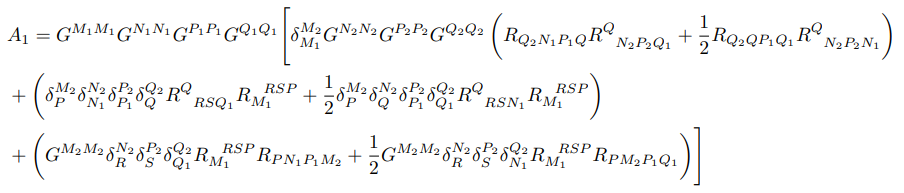
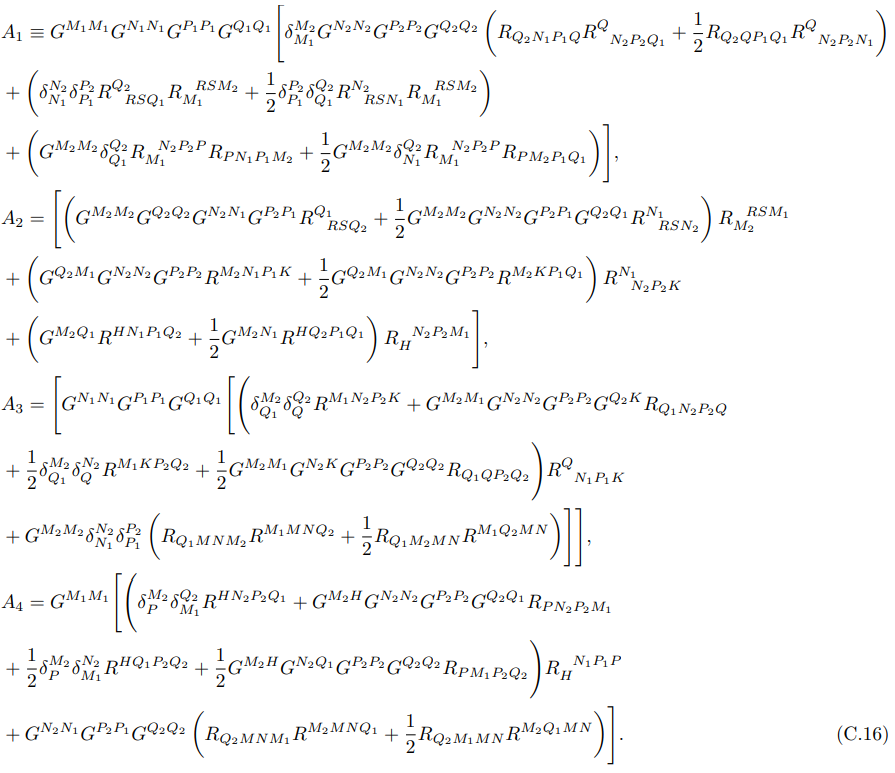
• To derive the equation of motion associated with embedding t(r), we must compute the derivatives that result from equation (7.56):

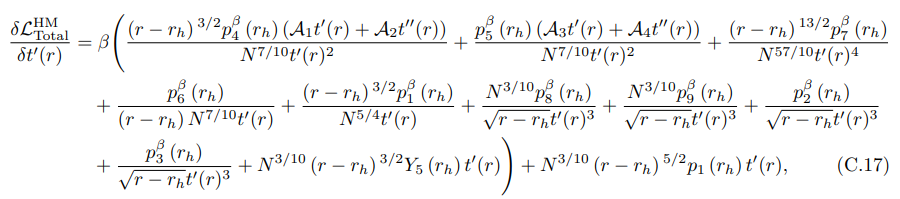
and

where

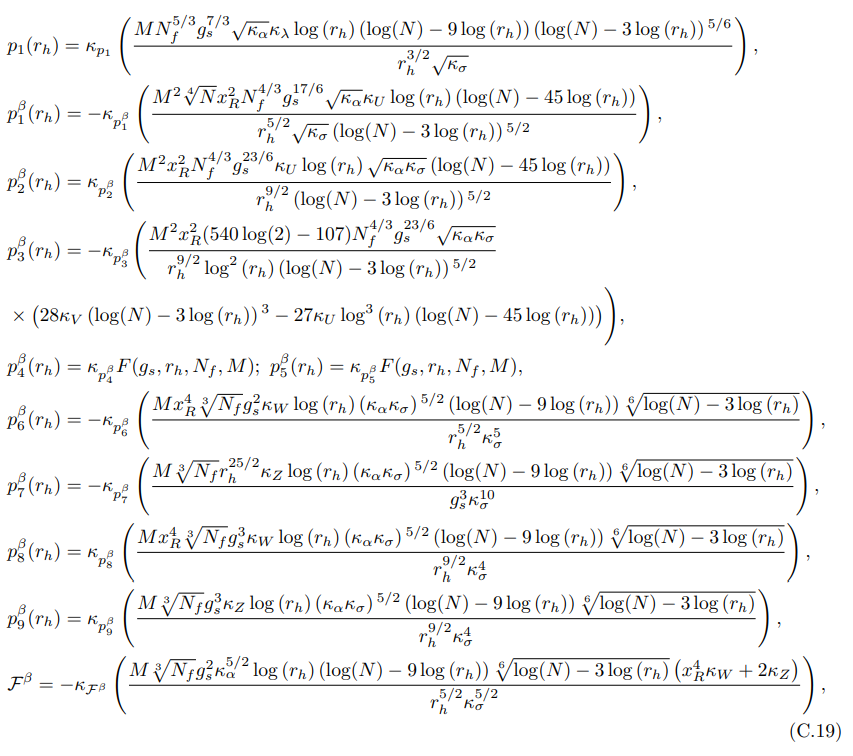
C.4 Island Surface Miscellania

We enumerate the many functions that emerge from the entanglement entropy of the island surface at O(β) in this appendix. We additionally calculated the derivatives of the Lagrangian associated with the island surface here, which were utilized to calculate the equation of motion concerning the island surface’s embedding.

• The following terms (λ3,4(r)) exist in the Wald entanglement entropy term (first term of holographic entanglement entropy (7.78)) of the island surface:

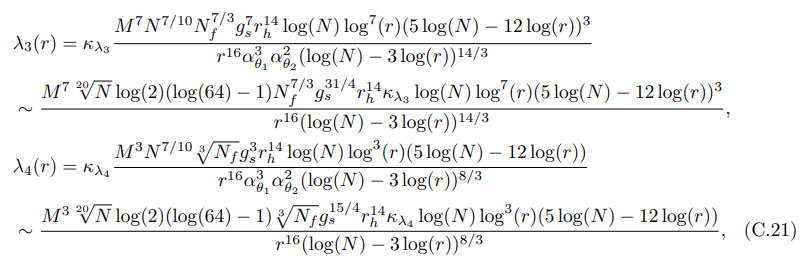
where κλ3 and κλ4 being the numerical factors.

• The r dependent functions appeared in the anomaly term (the second term of holographic entanglement entropy (7.78)) are as follows:

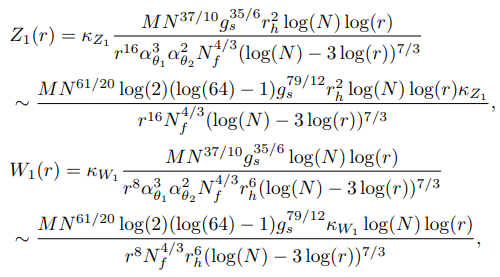
• For the action associated with the island surface’s embedding (7.79), we obtained:

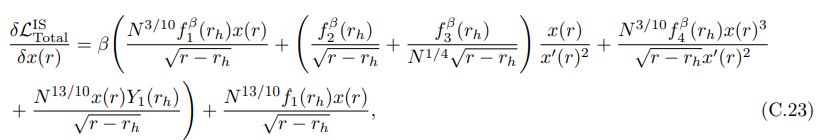
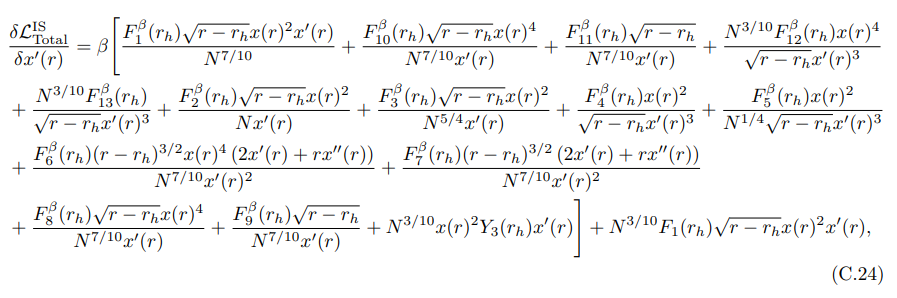
and,

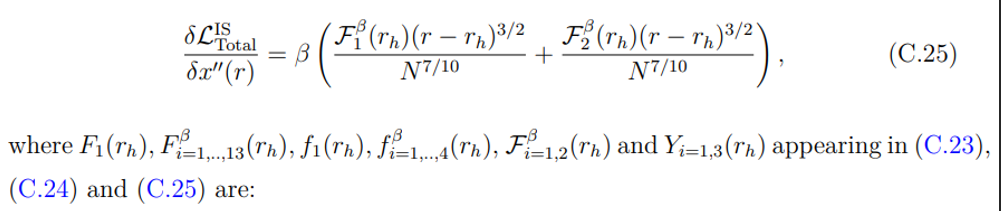
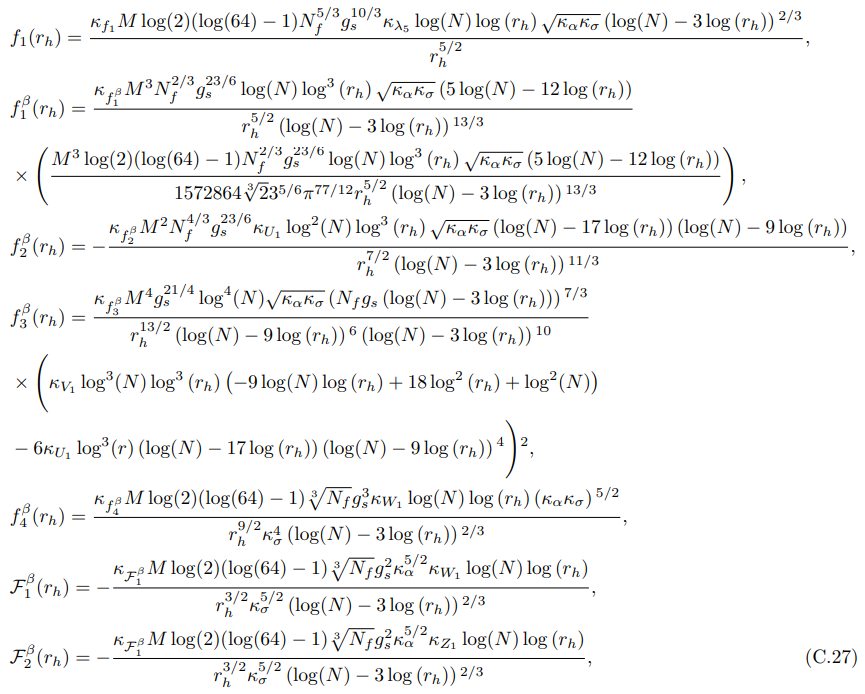
and,

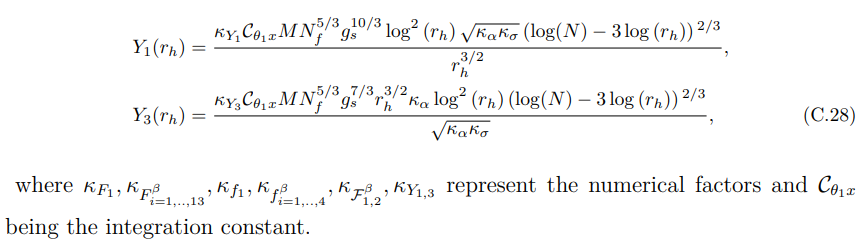
C.5 Possible Terms Appearing in Holographic Entanglement Entropies

Within this appendix, we provided all of the terms that could possibly be obtained by differentiating the Lagrangian of the M-theory dual, including O(R4 ) corrections. We have included all of the words associated with the Hartman-Maldacena-like surface in C.5.1, and all of the available terms of the island surface in C.5.2.

C.5.1 Hartman-Maldacena-like Surface

• √ −g Associated with the Induced Metric (7.23):

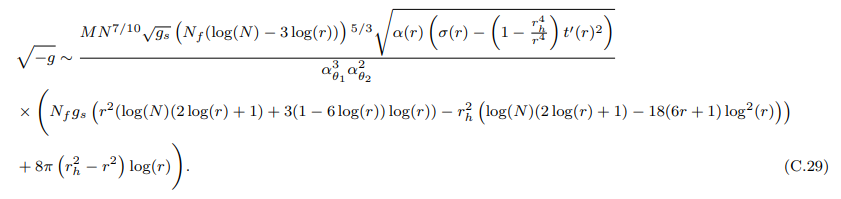
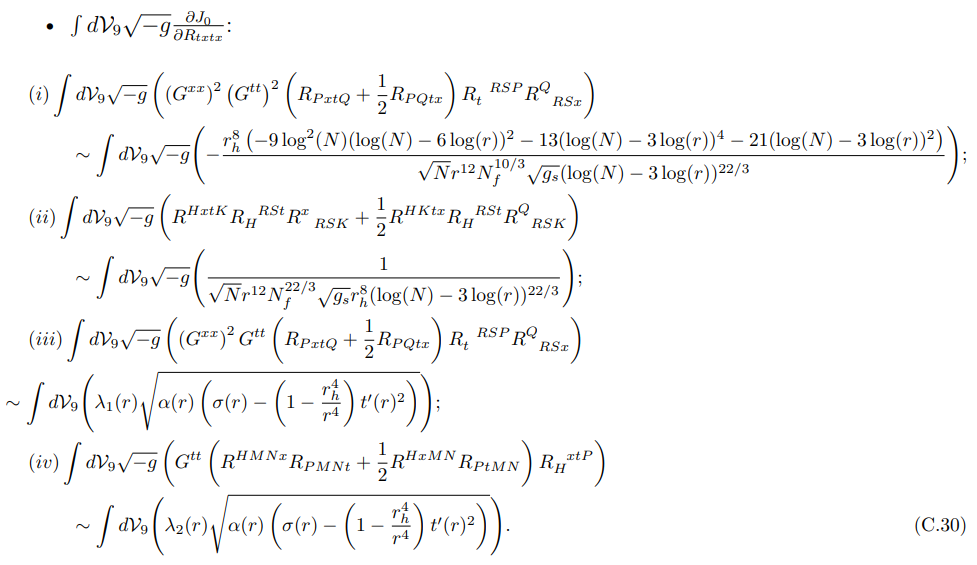
The equation (C.30) suggests that in the large-N limit, (iii) and (iv) terms correspond to the most dominant terms.

where there is no N dependence in G1(r) and G2(r). The terms (v) and (xii) are the most prominent in the large-N limit among all the terms stated above.

where G3(r) and G4(r) have no N dependence. The terms (v) and (xii) are the most dominant in the large-N limit.

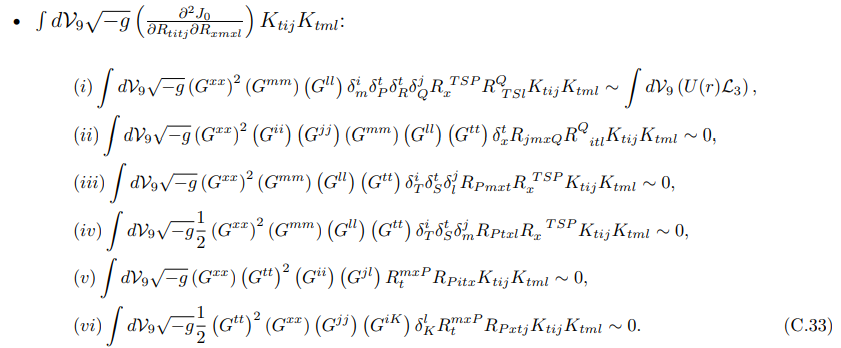
Since, only first term is non-zero, and hence this contributes to the Lagrangian.

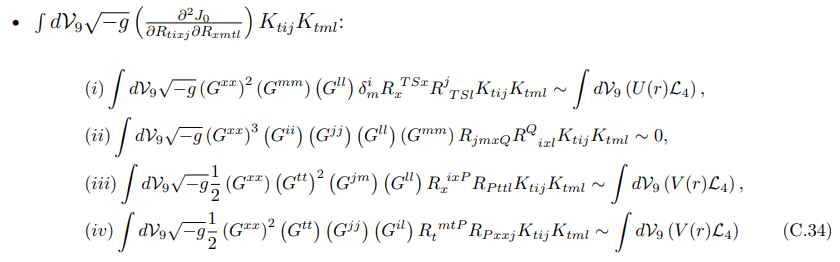
For the above equation, we found that all the three non-zero terms scale as N, and hence we kept all the non-zero terms in the Lagrangian.

C.5.2 Island Surface

• √ −g Associated with the Induced Metric (7.40):

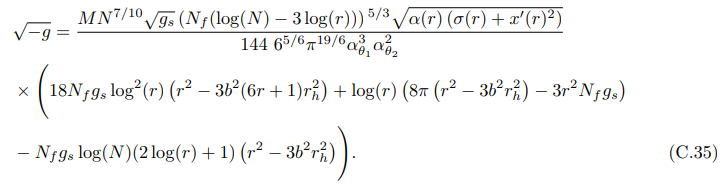
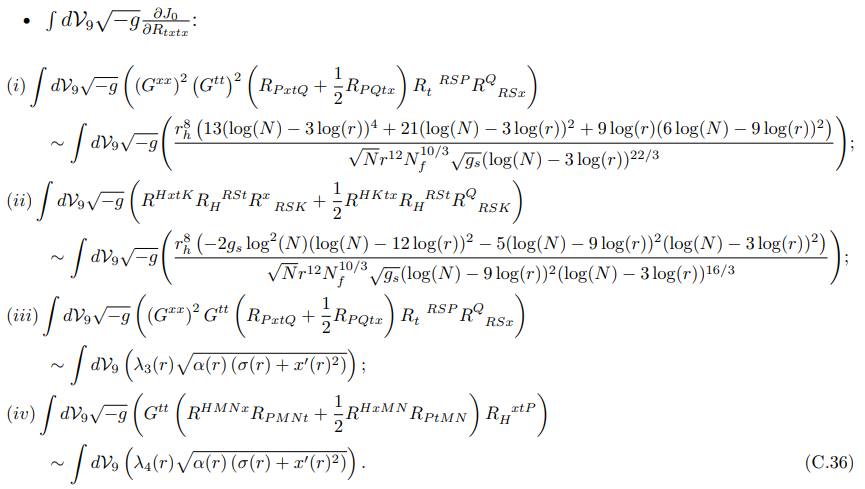
In the large N limit, terms (iii) and (iv) turn out to be the most dominant.

where G5(r) and G6(r) do not depend on N. We found that, terms (v) and (xii) dominate in comparison to other terms in the large N limit.

where G7(r) and G8(r) independent of N and the most dominant terms are (v) and (xii) in the larg-N limit.